Generic Types: Adding Math Puzzles To Your Code

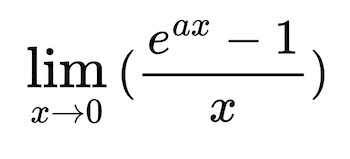
In this formula, x is the bound variable, a is
the free variable and e is constant.

Most modern, statically typed languages allow us to use generic types. We write a function once with generic type syntax, and then the compiler can apply the same code over and over again to different actual, concrete types. Hence the name generic.

This is a powerful language feature, but generic code is often confusing and hard to read. For me, generic code resembles something from my high school algebra textbook. I see small math puzzles sprinkled around my computer program. Why do this? Why add math problems to your code? Computer programming is already hard enough; why make it even more complicated?

Generic types allow us to get the best of both words: the safety and performance of static types, with the flexibility and simplicity of a dynamic, typeless language.

But this comes at a steep price: Using generic types force you to write two programs, in a sense. Your normal code for runtime, and a second, parallel type-specific program that runs at compile time. To see what I mean, let’s take an example from the Crystal standard library and explore how the Crystal team used generic type syntax to implement their array class.

Array#uniq in Crystal

Last time I looked at the Crystal standard library, specifically at how Crystal removes duplicate elements from an array in Array#uniq. I discussed a couple of optimizations the Crystal team used to implement uniq for small or empty arrays.

But what about the general case? How does Crystal remove duplicate elements from large arrays? If I remove the small array optimizations, the Crystal implementation of Array#uniq reads like this:

class Array(T)

  def uniq
    # Convert the Array into a Hash and then ask for its values
    to_lookup_hash.values
  end

  protected def to_lookup_hash
    to_lookup_hash { |elem| elem }
  end

  protected def to_lookup_hash(& : T -> U) forall U
    each_with_object(Hash(U, T).new) do |o, h|
      key = yield o
      unless h.has_key?(key)
        h[key] = o
      end
    end
  end

end

This is almost easy to read. Admittedly, I’m a Ruby developer, so the Ruby-like syntax makes perfect sense to me. However, most developers will be able to figure this out without much effort.

Crystal identifies the unique elements of the array by converting it into a “lookup hash:”

As you know, hash keys are unique. By converting the array into a hash, Crystal has quickly identified the unique elements of that array.

Converting An Array To A Hash At Runtime

But if you read carefully, you’ll see that Crystal converts the array to a hash twice: once at compile time and then later again at runtime. Let’s look at the second, runtime program first, working our way from the inside out.

First, the unless clause inside the loop checks whether the hash already contains a given element. If the element isn’t already in the hash, Crystal adds it:

unless h.has_key?(key)
  h[key] = o
end

This is the crux of the unique algorithm. Crystal won’t insert a given key value twice. (Although the unless clause is technically unnecessary; saving a repeated value would be harmless, overwriting the previous copy in the hash.)

Looking up one line, we can see the to_lookup_hash function accepts a block, and calls it to calculate the a key value for each array element:

key = yield o
unless h.has_key?(key)
  h[key] = o
end

And reading farther up, we can see another definition of to_lookup_hash passes in such a block:

protected def to_lookup_hash
  to_lookup_hash { |elem| elem }
end

Since the block { |elem| elem } just returns whatever was passed into it, the keys and values of the lookup hash will be the same:

This block adds a bit of flexibility to the code. The Crystal team might want to reuse this function someday with a different block and set of keys.

Finally, let’s look at how Crystal iterates over the array:

each_with_object(Hash(U, T).new) do |o, h|
  key = yield o
  unless h.has_key?(key)
    h[key] = o
  end
end

Crystal calls each_with_object on the array and provides a single argument: Hash(U, T).new. Here’s our first example of generic type syntax. I’ll come back to that in a moment. For now, I can guess that Hash(U, T).new creates a new, empty hash.

Next, each_with_object loops over the receiver (the array), and calls the block do |o, h| … end for each element. It sets o to each element’s value as it iterates, and h to the hash created with Hash(U, T).new. As we saw above, the block inserts each value o into the hash h, skipping duplicates.

Finally, after the iteration completes, Crystal returns the values from the new hash, a new array containing only the unique elements from the original array:`

to_lookup_hash.values

Converting An Array To A Hash At Compile Time

But there’s more to this program than meets the eye. Crystal actually runs part of this code, the generic type syntax, earlier at compile time. And, curiously, that code also converts the array into a hash but in a different way. When the Crystal team wrote Array#uniq, they had to write two programs, not one!

What exactly do I mean by “converting an array to a hash at compile time?” How and why does this happen? And what’s the second program here?

The answer has to do with the Hash(U, T).new expression we read above. Crystal needs to convert the type Array(T) into the type Hash(U, T). Let’s step through the second, type-level mirror program to find out how this works.

You can imagine the Crystal compiler processing the generic type code like this:

The first line is actually the most important:

class Array(T)

This line means the Crystal team is not implementing a simple array of elements. Instead, they are implementing an array that must contain elements of the same type. And here on this line they name that type in a generic way: the type variable T.

Specifying an array element type provides two important benefits: First, it is a nice safety net for us, the developers using Crystal arrays. Crystal’s compiler will prevent us from accidentally inserting elements from a different or unexpected type into the array. And the best part is that Crystal will tell us about our mistake at compile time, before our code ever runs and does any harm with real data. It’s annoying and difficult to write a second compile-time program using types, but the compiler might - and probably will - find some of our mistakes and tell us before the program even runs.

Second, because Crystal knows that all of the elements of the array have the same type, it can emit more efficient code that takes advantage of this knowledge. The machine language code the compiler produces can save and copy array elements faster because it knows how much memory each element occupies.

And by using generic type syntax to write Array#uniq, the Crystal team gives us these benefits regardless of what kind of elements we add to our arrays. The Crystal compiler automatically maps the type we happen to choose in our code to the variable T.

Next, take a look at the to_lookup_hash function declaration:

protected def to_lookup_hash(& : T -> U) forall U

What in the world does this mean? What is forall U referring to?

The first thing to note here is Crystal’s block parameter syntax: & : T -> U. Crystal has borrowed the & character from Ruby to indicate the following value is a block or closure, not a simple value. But in Crystal, the block parameters and the block’s return value all must have types. And here in this code those types are generic types: T and U. The arrow syntax tells us that the block takes a single parameter of type T, and returns a single value of type U.

But what do T and U mean? Where are they defined?

This is our math puzzle for the day. Just like in a limit, integral or infinite series from Calculus, this formula contains bound and free variables:

& : T -> U forall U

Since the enclosing class statement above declared the class to be Array(T), Crystal binds the T type variable here to be the same type as above. In order words, the type of values passed into this block must be the same as the type of the elements in the array.

But what about U? What type is that?

The forall U clause declares the U type to be a free variable. That means that U, unlike the type T, is not bound to any known type value. forall tells the Crystal compiler that the following code should apply equally well to any type U, “for all” possible types U.

The Crystal compiler solves this math puzzle using the yield statement we saw above:

key = yield o

Here Crystal knows the value o has a type of T. How? Because Crystal knows that all of the elements of the array have a type T, (this is the Array(T) class) and Crystal knows the variable o was set earlier to an array element by each_with_object.

Next, the Crystal compiler can determine that U == T, that both types are the same. How? When Crystal compiles the block’s code above:

to_lookup_hash { |elem| elem }

…Crystal notices that the return value of the block is the same as the value passed into the block, that elem == elem. Then, the Crystal compiler maps this return value to the block declaration: & : T -> U. Because Crystal knows elem == elem in the block code, it deduces that the types of these values are also the same, that U == T.

Finally, let’s return to the line above that iterates over the array:

each_with_object(Hash(U, T).new) do |o, h|

Now the Crystal compiler can use the knowledge that types U == T when it creates the lookup hash. In Crystal when you create a hash, just as when you create an array, you have to provide a type parameter for all the values. And for hashes you also need to provide a type for the keys. Hash(U, T).new means: Create a new hash which has keys of type U and values of type T.

Armed with the knowledge that the keys of the lookup hash all have type U, and that U == T, the Crystal compiler can emit the correct, optimized code for finding and inserting hash values when it produces machine language instructions for this passage:

key = yield o
unless h.has_key?(key)
  h[key] = o
end

Crystal knows that both o and key have the same type T, which allows the has_key? and []= methods to run quickly and correctly.

Are Generic Types Worth It?

It’s a good thing the Crystal compiler is good at solving math puzzles! Crystal, like many other modern languages (Haskell, Swift, Rust, etc.) is able to determine the actual, concrete types for variables like T and U, and for all values in your code, using type inference. The Crystal compiler can deduce what the type of each variable is based on the usage of that variable and the context of the surrounding code.

But the problem is that I, a user of the Crystal language, have to be good at math puzzles also. As we’ve just seen, in order to write code using Crystal or any language with a modern type system, I have to write my code twice: once to solve the problem I actually want to solve, and a second time to prove to the compiler that my code is consistent and mathematically correct at a type level.

Are the added performance and added safety worth it? That depends entirely on what code you are writing, how fast it needs to run, how many times and for how long that code will be used - and most importantly, how much time you have to solve math problems.