How Big is a Bignum?

Ruby represents small integers using Fixnum
and large integers using Bignum.

Most of us don’t use Ruby to perform complex calculations for science, engineering or cryptography applications; instead, we might turn to R, Matlab or some other programming language or tool for that sort of thing. When we calculate values using Ruby, it’s often to process simple values while generating a web page using ERB or Haml, or to handle the result of a database query using ActiveRecord. Almost all of the time, Ruby’s Fixnum class is more than sufficient.

For most Ruby developers, therefore, the Bignum class is a dark, unfamiliar corner of the language. Today I’d like to shed some light on Bignum by looking at how Ruby represents integers internally inside the Fixnum and Bignum classes. What’s the largest integer that fits inside a Fixnum; just how big is a Bignum?

Also, it turns out that Ruby 2.1 contains an important new change for the Bignum class: support for the GNU Multiple Precision Arithmetic Library (GMP) library. In my next post, I’ll take a look at mathematical theory and history behind some of the algorithms used by Bignum internally and how Ruby 2.1 works with GMP. But for now, let’s start with the basics.

64-Bit Integers

Most computers these days represent numbers as 64 digit binary values internally. For example, the number ten thousand looks like this expressed as a binary value:

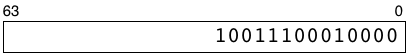
My rectangle here represents how a 64-bit computer would save an integer in a microprocessor register or a RAM memory location. The numbers 63 and 0 indicate that there are spaces for 64 binary digits, each of which can contain a zero or one. The most significant binary digit, #63, is on the left, while the least significant digit, #0, is on the right. I’m not showing all of the leading zeroes here to keep things simple.

The term 64-bit architecture means the logic gates, transistors and circuits located on your microprocessor chip are designed to process binary values using 64 binary digits like this, in parallel. Whenever your code uses an integer, the microprocessor retrieves all of these on/off values from one of the RAM chips in your CPU using a “bus” or set of 64 parallel connections.

64-Bit Integers in MRI Ruby

The standard implementation of Ruby, Matz’s Ruby Interpreter (MRI), saves integers using a slightly different, custom format; it hard codes the least significant digit (on the right in my diagram) to one and shifts the actual integer value one bit to the left. As we’ll see in a moment, if this bit were zero Ruby would instead consider the integer to be a pointer to some Ruby object.

Here’s how Ruby represents ten thousand internally:

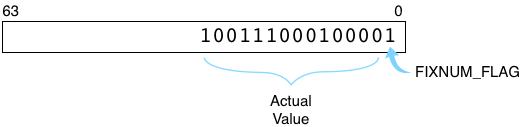
FIXNUM_FLAG=1 indicates this integer represents an instance of the Fixnum class. The flag is a performance optimization, removing the need for Ruby to create a separate C structure the way it normally would for other types of objects. (Ruby uses a similar trick for symbols and special values such as true, false and nil.)

Two’s Complement in Ruby

Like most other computer languages and also like your microprocessor’s actual hardware circuits, Ruby uses a binary format called two’s complement to save negative integers. Here’s how the value -10,000 would be saved inside your Ruby program:

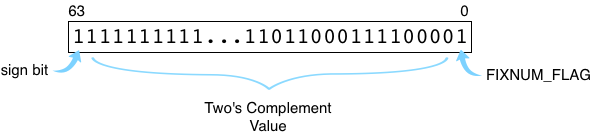
Note the first bit on the left, the sign bit, is set to 1. This indicates this is a negative integer. Ruby still sets the lowest bit, FIXNUM_FLAG, to 1. The other bits contain the value itself. To calculate a two’s complement value for a negative integer, your microprocessor adds one to the absolute value (getting 10,001 in this example) and then reverses the zeroes and ones. This is equivalent to subtracting the absolute value from the next highest power of two. Ruby uses two’s complement in the same way, except it adds FIXNUM_FLAG on the right and shifts the rest of the value to the left.

The Largest Fixnum Value: 4611686018427387903

Using 64-bit binary values with FIXNUM_FLAG, Ruby is able to take advantage of your computer’s microprocessor to represent integer values efficiently. Addition, subtraction and other integer operations can be handled using the corresponding assembly language instructions by removing and then re-adding FIXNUM_FLAG internally as needed. This design only works, however, for integer values that are small enough to fit into a single 64-bit word. We can see what the largest positive Fixnum integer must be by setting all 62 of the middle bits to one, like this:

Here we have a zero on the left (indicating this is a positive integer) and a one on the right (for FIXNUM_FLAG). The remaining 62 bits in the middle hold this binary number:
11111111111111111111111111111111111111111111111111111111111111

Converting this to decimal we get: 4611686018427387903, the largest integer that fits into a Fixnum object. (If you compiled Ruby on a 32-bit computer, of course, the largest Fixnum would be much smaller than this, only 30-bits wide.)

The Smallest Bignum: 4611686018427387904

But what does Ruby do if we want to use larger numbers? For example, this Ruby program works just fine:

But now the sum doesn’t fit into a 64-bit Fixnum value, since expressing 4611686018427387904 as a binary value requires 63 digits, not 62:

This is where the Bignum class comes in. While calculating 4611686018427387903+1, Ruby has to create a new type of object to represent 4611686018427387904 - an instance of the Bignum class. Here’s how that looks inside of Ruby:

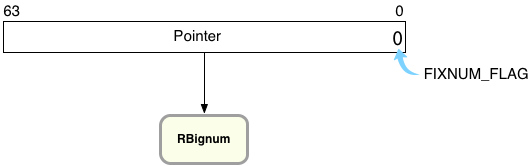
On the right you can see Ruby has reset the FIXNUM_FLAG to zero, indicating this value is not a Fixnum but instead a pointer to some other type of object. (C programs like MRI Ruby that use malloc to allocate memory always get addresses that end in zero, that are aligned. This means the FIXNUM_FLAG, a zero, is actually also part of the pointer’s value.)

The RBignum Structure

Now let’s take a closer look at the RBignum C structure and find out what’s inside it. Here’s how Ruby saves the value 4611686018427387904 internally:

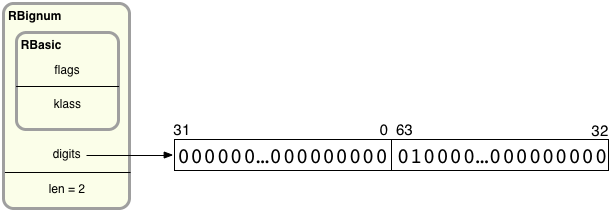
On the left, you can see RBignum contains an inner structure called RBasic, which contains internal, technical values used by all Ruby objects. Below that I show values specific to Bignum objects: digits and len. digits is a pointer to an array of 32-bit values that contain the actual big integer’s bits grouped into sets of 32. len records how many 32-bit groups are in the digits array. Since there can be any number of groups in the digits array, Ruby can represent arbitrarily large integers using RBignum.

Ruby divides up the bits of the big integer into 32-bit pieces. On the left, the first 32-bit value contains the least significant 32 bits from the big integer, bit 31 down to bit 0. Following that, the second value contains bits 63-32. If the big integer were larger, the third value would contain bits 95-64, etc. Therefore, the large integer’s bits are actually not in order: The groups of bits are in reverse order, while the bits inside each group are in the proper order.

To save a Bignum value, Ruby starts by saving the least significant bits of the target integer into the first 32-bit digit group. Then it shifts the remaining bits 32 places to the right and saves the next 32 least significant bits into the next group. Ruby continues shifting and saving until the entire big integer has been processed.

Ruby allocates enough 32-bit pieces in the digits array to provide enough room for the entire large integer. For example, for an extremely large number requiring 320 bits, Ruby could use 10 32-bit values by setting len to 10 and allocating more memory:

In my example Ruby needs just two 32-bit values. This makes sense because, as we saw above, 4611686018427387903 is a 62-bit integer (all ones) and when I add one I get a 63-bit value. When I add one, Ruby first copies the 62 bits in the target value into a new Bignum structure, like this:

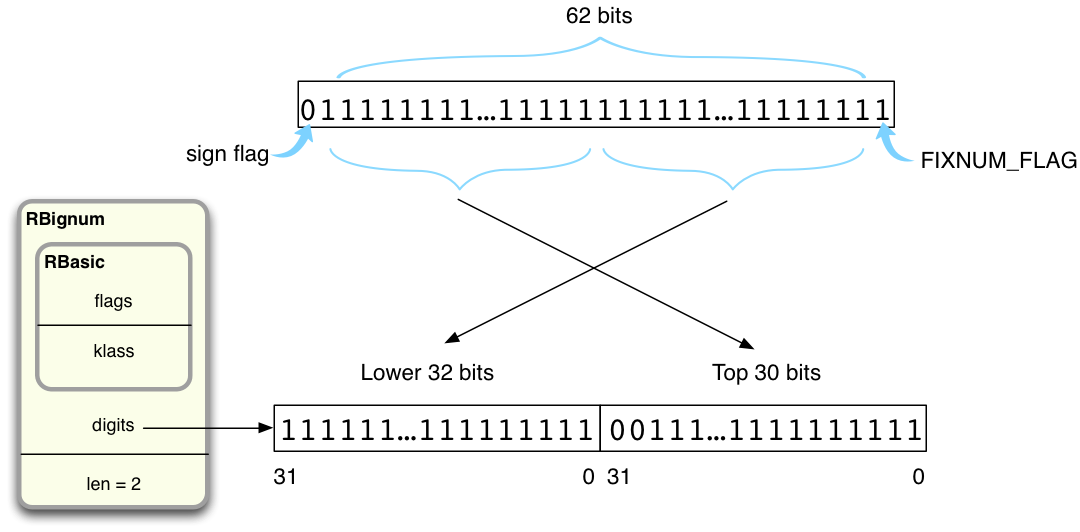
Ruby copies the least significant 32 bits into the first digit value on the left, and the most significant 30 into the second digit value on the right (there is space for two leading zeroes in the second digit value).

Once Ruby has copied 4611686018427387903 into a new RBignum structure, it can then use a special algorithm implemented in bignum.c to perform an addition operation on the new Bignum. Now there is enough room to hold the 63-bit result, 4611686018427387904 (diagram copied from above):

A few other minor details to learn about this:

• Ruby saves the sign bit inside the RBasic structure, and not in the binary digit values themselves. This saves a bit of space, and makes the code inside bignum.c simpler.
• Ruby also doesn’t need to save the FIXNUM_FLAG in the digits, since it already knows this is a Bignum value and not a Fixnum.
• For small Bignum’s, Ruby saves memory and time by storing the digits values right inside the RBignum structure itself, using a C union trick. I don’t have time to explain that here today, but you can see how the same optimization works for strings in my article Never create Ruby strings longer than 23 characters.

Next time

In my next post I’ll look at how Ruby performs an actual mathematical operation using Bignum objects. It turns out there’s more to multiplication that you might think: Ruby uses one of a few different multiplication algorithms depending on how large the integers are, each with a different history behind it. And Ruby 2.1 adds yet another new algorithm to the mix with GMP.