What does (((λ f . (λ x . (f x))) (λ a . a)) (λ b . b)) mean?

This week I’ve been spending some free time between projects working on my function programming skills. I’m a Ruby developer but have always been fascinated by functional languages such as Haskell, Clojure and of course Lisp. I was excited this morning when I stumbled across a fascinating article called 7 lines of code, 3 minutes: Implement a programming language from scratch. The author, Matthew Might, touches on Lambda Calculus notation before implementing a simple interpreter for Lambda Calculus using just seven lines of Scheme code. He later proceeds to write a Scheme interpreter in about 100 lines of code, using a dialect of Scheme called Racket.

Matthew starts by introducing the basics of Lambda Calculus notation like this:

Matthew explains that all of Lambda Calculus is based on these two simple concepts, along with variable references. He then shows a couple of simple examples:

...and then asks the reader this simple question:

In this post I’ll try to answer this question using a series of diagrams. I’m a visual learner, and teacher. For me drawing something makes it much easier to understand and to explain to someone else. Lambda Calculus experts (“Lambda Mathematicians?”) probably have accepted styles for drawing these concepts which I’m not aware of. I’ll just draw what comes naturally to me.

Getting Rid of All Those Parentheses

If I had a whiteboard, I’d rewrite the complex Lambda Calculus expression above with circles instead of parentheses. This makes it much easier for me to see the nesting and order of operations. An even better visualization might be a tree structure, but I'll keep things inline with cirlces today.

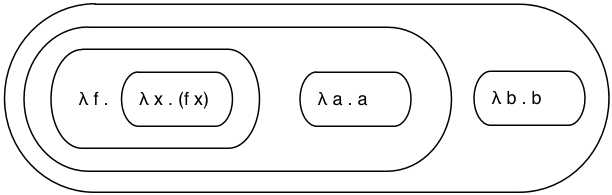
For me, the biggest challenge to understanding Lisp or Scheme has always been all the nested parentheses. This picture is still cryptic and meaningless, but now at least I can see the order of operations and nesting more easily.

Start From the Inside and Work Your Way Out

To understand what’s going on here, I started with the innermost lambda expression:

Referring to Matthew’s explanation above, (f x) means evaluate the function f on the argument x. Therefore, this expression represents an anonymous function that applies some function f to its argument, x. The oval on the left is the function and I’ve written this explanation on the right: what the function does.

I usually visualize functions with inputs and outputs, like this:

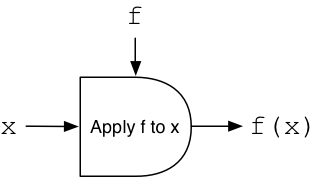
Here you can see the input x comes from the left, and I’ve shown the anonymous function in the center using a half-oval. It applies a function f, which is almost like a second input value, to x and returns an output value on the right.

Higher Order Functions

Now let’s substitute this simple function back into the complex expression:

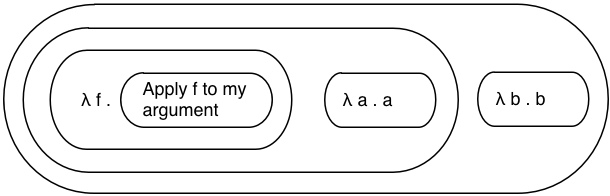
You can see I’ve pasted the text “Apply f to my argument” into the center of the expression where the previous lambda was located. Working my way out, let’s take a look at what the next lambda expression means:

Here you can see a definition for another anonymous function, another lambda expression, which takes f as an argument. The body of the function is our previous expression.

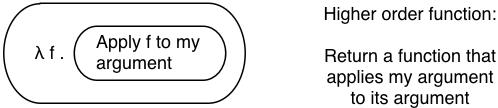
What this boils down to, therefore, is a function that takes a function as an argument and returns a second function as a result. Here’s what this might look like using my input/output diagram style:

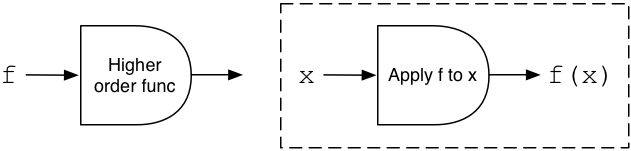
On the left you can see the function takes a function, f, as input. On the right the dashed rectangle represents a single output value: another function. This is an example of a higher order function, a function that can use other functions as inputs or outputs.

In this example, the output is a new function which applies f, the input of the higher order function, to its argument x. We don’t have a value for x yet, but we have a new function which later can take an input x. It will apply the present input, f, to whatever argument it receives later, x.

The other subtle detail to think about here is that above, when we looked at the innermost lambda expression, the value f was undefined. The inner lambda applied f to its input x, not knowing what f was. Now f has been provided by the surrounding expression, the outer lambda. f is the input to the outer lambda. I’m not sure about this, but I suspect lambda mathematicians would say the outer lambda is a closure around the free variable, f.

Identity Functions

Substituting again, here’s the entire expression simplified:

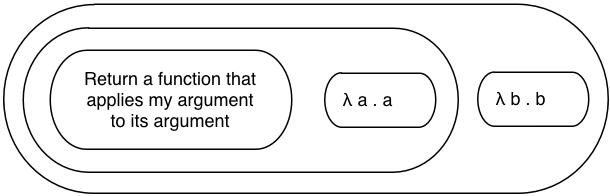
The two lambdas on the right are easier to follow. These are examples of the identity function, a function that returns its argument. Matthew showed this syntax as one of his examples.

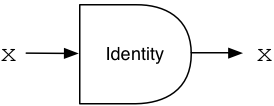
You can see here the identity function simply passes its input along as an output:

Evaluating a Function

Substituting again, here’s what we have now:

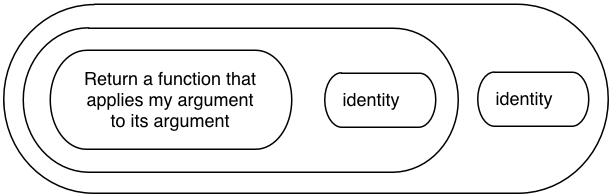
Earlier we saw the higher order function on the left returns a function that will later operate on an argument, which I showed as x. Now its time has come. Recall that (f x) in Lambda Calculus means “evaluate the function f on the argument x.”

In other words, this expression:

… means: “evaluate the higher order function on the left, providing the function on the right as an argument.”

The higher order function will take one function (the identity function) and return another:

The output is a new function which will apply the identity function (the argument) to its own argument x. Of course, this is equivalent to the identity function itself!

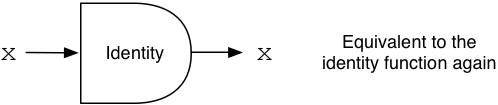
There must be some Lambda Calculus axiom (the “lambda identity axiom?”) behind this deduction, but I’m not sure. I’ll consider it obvious and just move on.

The Result

Substituting this result back into the original expression, we’re left with this:

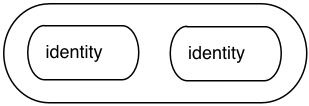
Reapplying the “lambda identity axiom” again it’s obvious this is equivalent to the identity function:

That is, the identity function is also a higher order function. It returns the same functions you pass to it, unchanged.

Stepping back and taking stock, we’ve deduced that:

(((λ f . (λ x . (f x))) (λ a . a)) (λ b . b))

Is equivalent to:

(λ x . x)

Or the identity function.

What Did I Get Wrong?

As I mentioned, I’m just learning about functional programming and lambda calculus. If you have some computer science training and see something wrong here, let me know. Or if you know the real name for the “lambda identity axiom” or have examples of better diagrams for representing lambda expressions, please pass along a link.