Ruby Multiplies Like a Fourth Grader
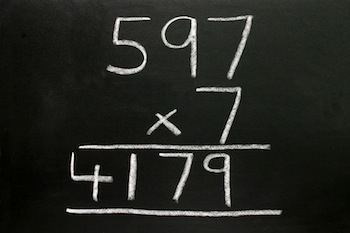
Ruby multiplies large integers using the same
algorithm we learned in elementary school.
Imagine yourself as an 8 or 9 year old at a chalkboard learning to multiply. Your teacher asks you to write one number over another, and then to draw an “x” and a line below. Next you multiply the numbers one digit at a time, using the multiplication table you memorized the year before. Your teacher also shows you how to “carry” values from one column to the next when they don’t fit as a single digit.
After studying Ruby’s multiplication algorithm, I was surprised to find out that Ruby multiplies large numbers (Bignum’s) the same way you learned in fourth grade: one “digit” at a time. My post today will give you a quick refresher course on fourth grade math, and then explain how Ruby’s Bignum class uses the same classic, long multiplication algorithm you learned in elementary school!
A Crash Course in Fourth Grade Math
We all remember multiplication tables: memorizing them was either a fun mental exercise - or a painful form of torture - depending on our mathematical aptitude and the personality of our grade school teacher. Regardless, there were two reasons for memorizing simple products such as 5 x 6 = 30 or 9 x 7 = 63. First, these simple problems occur frequently; and second, they help us later when multiplying larger numbers.
Maybe you flunked out of school before the fourth grade, or more likely you’ve become so dependent on your iPhone’s calculator app you don’t remember how to multiply by hand. Before we look at how Ruby multiplies numbers, let’s review the classic long multiplication algorithm.
Here’s a sample problem:
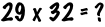
Now walk up to the chalkboard and write the two numbers one above the other, the larger number on top:
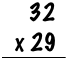

Remember what to do next? For me fourth grade was in the 1970s, but somehow it still comes back to me! Start by multiplying the rightmost digits from each number together (2 x 9 = 18), placing the product below the line:
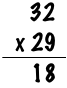
However, since 18 is too large to fit into a single digit you “carry” the 1 up to the top of the next column, and leave the 8 behind:
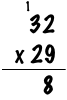
Next multiply 9 again by the next digit from the top number, 3 in this example, adding the 1 you carried from the last step. So you calculate (9x3)+1 = 28.
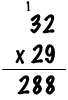
Here I’ve written the 28 below the line, to the left of the previous 8 value. So far you’ve calculated that 9x32 = 288.
Remember what to do next? I know it’s been a long time! Repeat the process with the next digit from the lower number, 2. In other words, you calculate 2x32=64. However, this time you write the product farther below, shifted to the left like this:
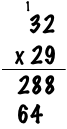
You shift the numbers to the left because the 2 from 29 is actually a 20. Now all you need to do is add the two intermediate products together, like this:
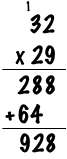
Drop the first 8 down, add 8+4=12, carry the 1 and finally calculate 1+2+6 = 9. You have the answer, 928. Congratulations, you’ve managed to multiply two numbers by hand without a calculator!
Ruby’s Multiplication Table
To multiply small numbers Ruby doesn’t implement a software algorithm. Instead, Ruby relies on your computer’s microprocessor’s hardware circuits to perform the calculation. Your microprocessor, in a sense, plays the role of a multiplication table for Ruby. By using a machine language instruction to multiply numbers, Ruby can get simple products very quickly. This is loosely analogous to you or I memorizing the simple products from the multiplication table in our heads.
As I discussed in my last article, Ruby stores small integers as native 64-bit values using the Fixnum class. For example, in Ruby we could multiply two numbers like this:

When you execute this program, Ruby’s internal C code represents these two numbers as Fixnum objects:

As you can see, Ruby represents each Fixnum with a 64-bit binary value with the least significant bit (FIXNUM_FLAG) set. When it needs to multiply, Ruby first removes the FIXNUM_FLAG bit and is left with the actual binary values 5 and 6. Now it can perform the multiplication using a native machine language instruction.
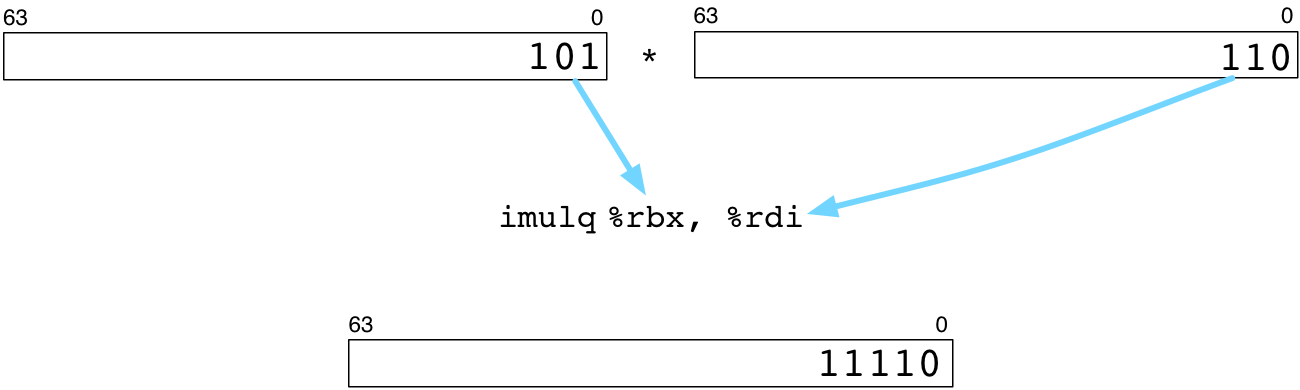
Above imulq is the Intel x86-64 assembly language instruction for multiplying integers. Ruby relies on the microprocessor to calculate 5x6 and to return the product 30, shown as binary at the bottom.
A Fourth Grader That Knows Hexadecimal
Ruby multiplies large numbers exactly the same way you and I do, using the classic long multiplication algorithm. We use long multiplication to multiply numbers larger than 12, since the multiplication tables we memorized went up to 12. Ruby uses long multiplication for numbers that don’t fit into a Fixnum object - numbers so large that a single machine language instruction can’t process them.
Here’s an example problem:
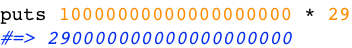
The number 29 fits into a Fixnum no problem, but 10000000000000000000 does not. Instead, Ruby represents this large integer using a Bignum object, like this:

You can see a simplified view of the RBignum C structure at the top. The digits pointer saves the location of an array of 32-bit values, the “digits.” As I explained in my last article, the digits are actually out of order, with the lower 32 bits on the left and the top 32 bits on the right.
Since Ruby represents Bignum’s with a complex data structure and not simple 64-bit integers, it can’t use machine language instructions to perform mathematical operations on them. What does Ruby do instead? How did it calculate 10000000000000000000 * 29 above?
It turns out Ruby uses long multiplication, just as we did in fourth grade! The only difference is that Ruby uses 32-bit “digits,” instead of digits that contain decimal values from 0-9.
To see what I mean, here’s another look at the 32x29 problem we did earlier:
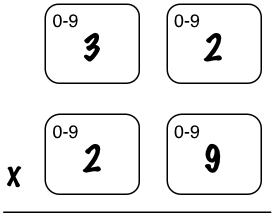
Above I show a rectangle around each 0-9 decimal digit. Remember the long multiplication algorithm works on one pair of digits at a time. The 0-9 notation means that each digit can hold a value between 0 and 9.
Now let’s take another look at the large integer multiplication Ruby executed above:

If I redraw this using 32-bit “digits,” I get this:
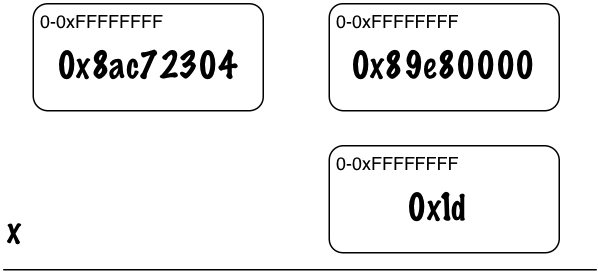
Each rectangle is a 32-bit word present in a Bignum digit data structure. At the bottom we see 0x1d, which is 29. (This does fit into a Fixnum but Ruby moves it to a Bignum before the multiplication starts.) Above that are the bits from the RBignum structure, shown in the proper order. 0x8ac72304 are the most significant 32 bits and 0x89e80000 are the least significant 32 bits. In order words, the hexadecimal value 0x8ac7230489e80000 is equivalent to 10000000000000000000.
It might seem bizarre to show a multiplication problem this way, but remember Ruby is a very special fourth grader, one that knows how to perform binary math and can understand hexadecimal.
Multiplying Bignums Using Long Multiplication
Once we’ve drawn the problem using 32-bit hexadecimal digits, we’ll be able to see that Ruby performs long multiplication just like you or I did back in school. First, it multiplies the rightmost digits from each number.
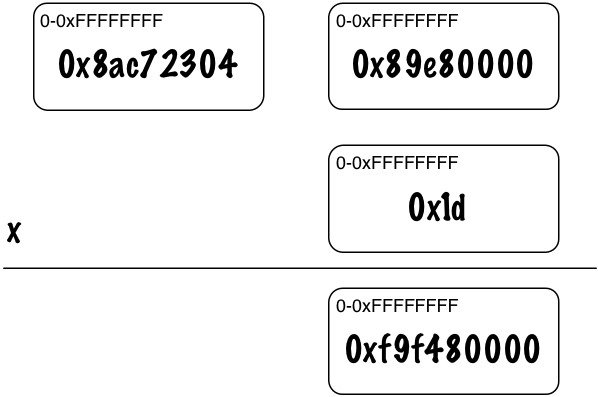
So we have 0x89e80000 * 0x1d = 0xf9f480000. But now the top 4 bits, the 0xf, doesn’t fit into a single 32-bit value. So Ruby “carries” the 0xf to the next column.
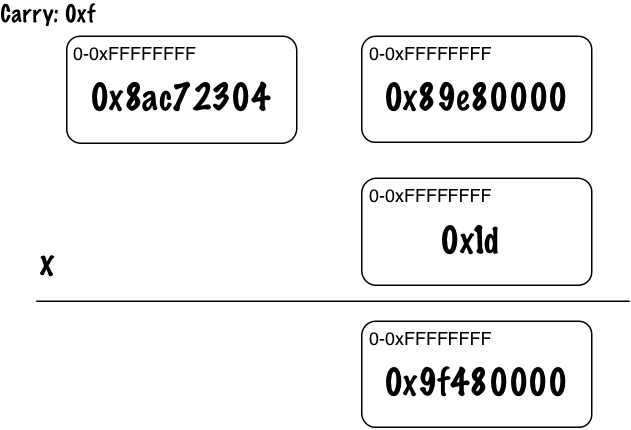
You can see above the carried value 0xf at the top left, and the remaining bits in the 32-bit digit at the bottom right.
Now Ruby calculates 0x8ac72304 * 0x1d + 0xf and gets 0xfb88ef783.

Once again, 0xfb88ef783 doesn’t fit into 32 bits, so Ruby carries the extra 0xf to the next column. Since this was the last column, Ruby is done and just moves the extra 0xf into a new 32-bit digit:
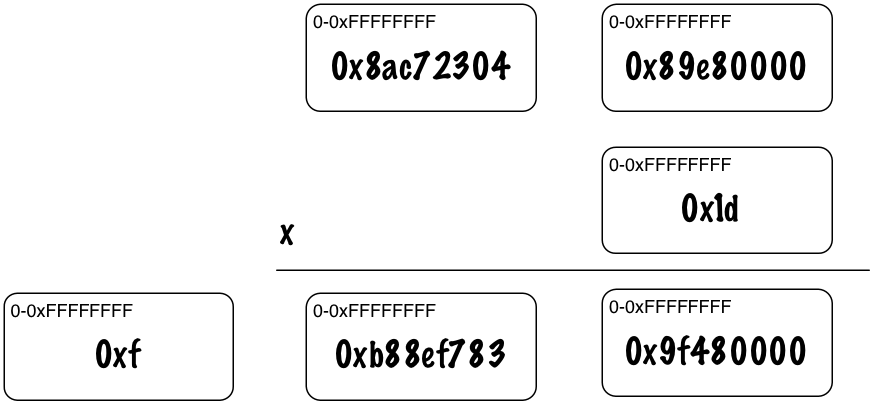
And now we have our answer:

Multiplication of Extremely Large Numbers
This was a very simple example, because 29 was actually a small integer. This meant Ruby didn’t need to use multiple rows in the long multiplication process, adding them together to get the final result. But Ruby would use multiple rows in long multiplication just the way we would if both numbers were large.
However, Ruby’s Bignum class was also designed to handle extremely large numbers that might contain thousands of digits. You might need these for certain scientific applications or in cryptography, for example. To handle extremely large numbers, the Bignum class also contains some alternative, advanced mathematical algorithms for multiplication, division and more. Ruby 2.1 also now optionally supports the GMP, the GNU Multiple Precision Arithmetic Library. In my next post I’ll take a look at how to enable GMP support and how to use it.


